Rotating Conducting Rod in B-field

The previous post outlined how to find the induced voltage across a moving metal rod in a B-field. Because of qv x B, we found the rod polarizes and therefore has an E-field and voltage difference because of a separation of charge. Here is a different situation. Suppose instead of moving linearly through the B-field, the metal rod is nailed down on one side, and rotates in the magnetic field?! It is a moving conductor, so we would still expect it to polarize, and therefore have a voltage difference across the rod. The trouble is, different points of the rod will have a different speed! How do we handle this situation? Check this out...

Moving a Conducting Rod through a B-field

Here's a case where by simply moving a metal stick through a magnetic field, the stick acts like a battery. The idea is that because it is a conductor, the rod has free electrons. By moving it in a B-field, we will have F = qv x B kick in. This causes the rod to become polarized, with one end positive and one end negative. But think about what else is set up if one separates charge on an object - you would have a voltage difference between the two ends. And if there is a voltage difference across a conductor, E = -dV/dr tells use there is an E-field running through the rod. This E-field produces an electric force on those same delocalized electrons. So a magnetic force points one way, and an electric force points in the opposite direction. At some point the electric force will balance the magnetic force, as long as the speed of the rod remains constant: qE = qvb.

I need student feedback.  For the how-to videos, is there a topic or problem that should have a video but does not?  Thanks for letting me know.

How to do LC Circuits - like Simple Harmonic Motion!

Here is an example of an LC circuit, where a charged capacitor is connected to an inductor.  The beauty of this circuit is that one can start an oscillating current (AC current).  This is the same as 'shaking' electrons, and this means electromagnetic waves are produced in the E-and B-fields.  These waves travel at the speed of light.  We will see that the math produces the same second-order differential equation we have in simple harmonic motion of oscillating springs!  So sines and cosines are the solutions to this equation.  Check it out!

SHM of Oscillating Stick due to Spring

Simple Harmonic Motion (SHM) is a periodic motion of some object caused by a restoring force that is proportional to the displacement, such as a spring.  Here is a different type of setup where a stick is lying on a frictionless table, with one end nailed to the table (which serves as the axis of rotation) and a spring attached near the other end of the stick.  If the stick is stretched slightly, so the stick forms a small angle relative to the vertical axis it had prior to stretching the spring, we can use the small angle approximation.  This says that for a small angle, the angle in radians is approximately equal to the sine of the angle.  Also, cosine of that small angle approaches 1.  We need both these approximations to solve this one!  Check it out.

A Very Cool Way of Looking at the Size Scales of the Universe

Check out this site, which is a very neat way of checking out the size scale of objects in the universe. It is similar to the classic Powers of Ten videos, but has better graphics. Enjoy!

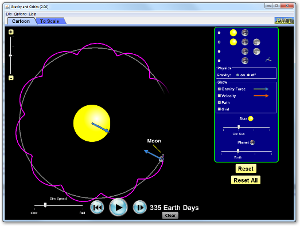
Cool PhET Simulation of Planetary Orbits

Check out this PhET simulation for a planet orbiting a star. Experiment with it by changing masses, adding a moon, etc. Very useful to see orbital motion in action!

Click to Run

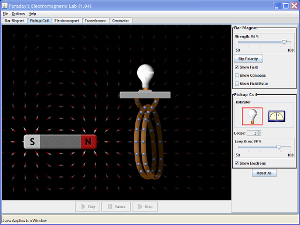
Faraday's law simulation

Here is a good visual for Faraday's law of em induction. Remember, it is all about changing magnetic flux! For more PhET physics simulations, go here.

Click to Run

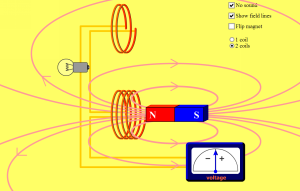
EM Induction Simulation

Here is a PhET simulation for electromagnetic induction applications. These are great for visualization of what em induction principles look like in the world. For many more physics simulations from PhET, go here.

Click to Run

Interesting Talk About Alternative Energy Production for the Grid

Donald Sadoway of MIT talks about an aspect of energy issues not normally focused on - batteries, or at least some way of storing energy created by solar and wind sources. If the sun is not out, and the wind not blowing, we need to have back-ups so we can continue to have access to energy. Our society simply demands this, and it will only increase as the population grows.

We will not be able to conserve enough, or drill enough, to continue to match increasing demands, so energy storage is the key to future energy production and consumption. Check out this TED talk. It is also a wonderful application of the chemistry and physics we are learning!