Every so often in physics we come across a slightly more complex function for a problem than what we are used to, and then need to find a derivative of that more complex function. By more complex I am referring to the case of 'compound functions,' which I define as an outside function operating on an inside function. A classic example happens with our solution to simple harmonic motion problems, where the position of a mass on a spring is defined as x(t) = Asin(wt + phi) or Acos(wt + phi), where A is amplitude, w is the angular frequency, and phi is a phase angle; these three are just constants. Here, we have an 'outside' function, sine or cosine, operating on an inside function, (wt + phi). How would you find the derivative of this compound function, which is necessary in physics if we want to find velocity and acceleration?
The answer is the Chain Rule. This says: the derivative is just the derivative of the outside function times the derivative of the inside function.
Check out a few examples in this video, and I suspect you will catch on within a few minutes. I hope this helps.
Saturday, April 19, 2014
Friday, April 18, 2014
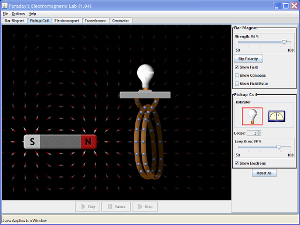
EM Induction Simulations: PhET
For visuals on EM Induction applications and contraptions, try this PhET simulation. You will get a sense of some induction properties and characteristics, so you have some good pictures in your heads as you do the mathematical details of these phenomena.
How to do the "Hardest Induction Problem Ever!"
I've given a problem to my students in E&M as a challenge problem - I call it the "hardest problem ever." It is a Faraday's law problem, where we have a circuit made of a bar sliding down a frictionless hill inside a constant magnetic field. This is the type of problem where the emf = -B dA/dt.
First, recognize that any problem where the area changes has the same answer for the emf: emf = Blv. This will be the case once again, as shown in the video. The challenging part of this is that, on a hill, there is a gravity component. There is also, in every type of problem like this where the area changes, a magnetic braking force (this tries to slow down the change in flux, and fits in with Lenz's law). If the magnetic braking force is the only force, it will slow the bar exponentially, like air friction on a hockey puck. But here, when there is a constant force trying to speed it up in addition to the magnetic braking force, we have a behavior like a sky diver - a terminal speed is reached!
Check out the details and see if it makes any sense.
First, recognize that any problem where the area changes has the same answer for the emf: emf = Blv. This will be the case once again, as shown in the video. The challenging part of this is that, on a hill, there is a gravity component. There is also, in every type of problem like this where the area changes, a magnetic braking force (this tries to slow down the change in flux, and fits in with Lenz's law). If the magnetic braking force is the only force, it will slow the bar exponentially, like air friction on a hockey puck. But here, when there is a constant force trying to speed it up in addition to the magnetic braking force, we have a behavior like a sky diver - a terminal speed is reached!
Check out the details and see if it makes any sense.
Tour of Doc V's Web Pages: School Page and Class Blog
This video is a bit different than the others - I simply want to make sure you know all the resources available to you on my class site on the school website, and what the most important pages on my class blog are. Check it out so you don't miss out on information that may be useful for you. And most importantly, if there are favorite sites of yours that you ever want to share with your classmates, just let me know the link and I'll get it on the site or blog. I hope this helps!
Sunday, April 13, 2014
How to do Biot-Savart for Multiple Currents - Yikes!!
Here it is...this can be for many students, the toughest part of magnetism. Biot-Savart (B-S) integrals for currents. Keep in mind B-S is the general law for finding magnetic fields from moving charges, and when there is a current, i.e. many moving charges, we need to add up a bunch of small B-fields to get the total - that means an integral!
Check out this video as an example for two currents. This means two magnetic fields, and therefore two integrals. Replay it as necessary, try to work along with it, to get the hang of constructing the integrals needed for a specific problem. Typically the thing that changes from problem to problem is the location of the point we are looking at, so that changes the bounds on the integrals. But the construction is pretty much the same process every time. FOCUS ON THE PROCESS used to construct each of the integrals, and that will help...that is the physics. I'm not even going to show the solutions of the integrals, because that is math; learn the physics here!
Check out this video as an example for two currents. This means two magnetic fields, and therefore two integrals. Replay it as necessary, try to work along with it, to get the hang of constructing the integrals needed for a specific problem. Typically the thing that changes from problem to problem is the location of the point we are looking at, so that changes the bounds on the integrals. But the construction is pretty much the same process every time. FOCUS ON THE PROCESS used to construct each of the integrals, and that will help...that is the physics. I'm not even going to show the solutions of the integrals, because that is math; learn the physics here!
How to do Biot-Savart (B-S) for Moving Point Charges
Perhaps the most challenging part of magnetism for students is Biot-Savart rule. This is the general rule that is used to find the strength and direction of magnetic fields created by moving charged particles or currents. In this video, the focus is on how to do B-S for point charges.
The B-S rule has a cross product in it, which is necessary due to the nature of Nature - Nature chose to have magnetic fields from moving charges circulate around that moving charge! How do we handle circulating vectors?!?!?! Well, you guessed it, with cross products.
The strength of the B-field from a moving charge ends up being B = (10^-7)qvsin(theta) / r^2. In this expression, theta is the angle between the motion of the particle (velocity) and the radial line from the charge to the point you are finding the B-field. What this means, by the way, is that magnetism is strongest at points perpendicular to the line of motion, and B = 0 if you are behind or in front of the moving charge, since sin(180) = 0 and sin(0) = 0, respectively.
Check out the examples, and hopefully this will help a bit.
The B-S rule has a cross product in it, which is necessary due to the nature of Nature - Nature chose to have magnetic fields from moving charges circulate around that moving charge! How do we handle circulating vectors?!?!?! Well, you guessed it, with cross products.
The strength of the B-field from a moving charge ends up being B = (10^-7)qvsin(theta) / r^2. In this expression, theta is the angle between the motion of the particle (velocity) and the radial line from the charge to the point you are finding the B-field. What this means, by the way, is that magnetism is strongest at points perpendicular to the line of motion, and B = 0 if you are behind or in front of the moving charge, since sin(180) = 0 and sin(0) = 0, respectively.
Check out the examples, and hopefully this will help a bit.
One Growth Profession - Cybersecurity
In class, when we were discussing your priorities if you were suddenly elected to Congress, the topic of cybersecurity came up. Personally, I would have rated this my top priority for those issues where science and technology are going to be the keys to finding viable solutions to the problem. Well, if you have any interest in computer science, computer engineering, and even law, it is predicted by the Information Trust Institute (at the U. of Illinois) that job growth in this sector of the economy will increase over 50% in the next few years. It is rare to see this sort of projected growth in any field nowadays, but if interested check out their Cyber Security Scholars Program.
Wednesday, April 9, 2014
How High to Start a Ball so it Rolls Around a Loop-the-Loop Without Falling Off
Here is a slight variation of another loop-the-loop problem, which typically is a block sliding down a hill and around the loop. Instead of just sliding with no friction, what if we put a ball on the track so it rolls without slipping...how will the height compare to that of the sliding block?
We would guess that, conceptually, a rolling ball might have to start higher than a block. Why? Because some energy is needed for the spinning of the ball. Without a boost in height, the translational speed of the ball will be too small to stay on the loop all the way around.
So check this out. It has rotations, circular motion, force diagrams, and conservation of energy all in one problem! I hope it makes a bit of sense for you.
We would guess that, conceptually, a rolling ball might have to start higher than a block. Why? Because some energy is needed for the spinning of the ball. Without a boost in height, the translational speed of the ball will be too small to stay on the loop all the way around.
So check this out. It has rotations, circular motion, force diagrams, and conservation of energy all in one problem! I hope it makes a bit of sense for you.
How High Does a Roller Coaster (block) have to Start to Make it Around a Loop?
Another classic mechanics problem involves a type of roller coaster problem. When you have a loop-the-loop, what is the minimum height on a hill the roller coaster, or in this case a block, have to start to just make it around the loop, without falling off?
This is a good problem primarily because it has some engineering overtones, but also because it combines circular motion with energy and a force diagram. It gives some decent insights of how mechanics principles are related and how to combine them. Check it out, and see if it makes sense.
This is a good problem primarily because it has some engineering overtones, but also because it combines circular motion with energy and a force diagram. It gives some decent insights of how mechanics principles are related and how to combine them. Check it out, and see if it makes sense.
A Classic: Bug on a Frictionless Bowling Ball
A popular problem is the "bug sliding down a frictionless bowling ball." The problem is to find the angle, relative to the vertical, at which the bug will just leave the surface of the ball. A more modern variation of this is a skier sliding down a frictionless, large snowball. This problem involves a combination of concepts, which is why it is so popular. Those key concepts include force diagrams, circular motion, and conservation of energy. It turns out the magic angle, which works for all masses and sizes of the ball, is cos(theta) = 2/3, or theta ~ 48 degrees. Check this out to see how it works out.
Monday, April 7, 2014
Congratulations to our two Moody's teams
ETHS is one of just a couple schools in the country to have both its teams in the Moody's Mega Math Challenge make the first cut and stay in the running for scholarships. Congratulations to Rebecca Conover, Micaela Homer, Rachel Kornbluh, Jordan Rosen-Kaplan, and Taylor Sims; and Benedict Brady, Emma Chanen, Justin Liao, Nikolai Lenney, and Henry McDonald. These teams are part of the top 200 in the country, with nearly 1200 submitted papers this year.
And then, just today, we found out that the team of Rebecca Conover, Micaela Homer, Rachel Kornbluh, Jordan Rosen-Kaplan, and Taylor Sims were one of only three schools in Illinois (the others being from Stevenson and Kaneland) to be rated nationally. This team is an Honorable Mention team, which only 5% of all teams nationally attain. They will split a $1000 scholarship for their efforts. Congrats to both teams for a job well done!
And then, just today, we found out that the team of Rebecca Conover, Micaela Homer, Rachel Kornbluh, Jordan Rosen-Kaplan, and Taylor Sims were one of only three schools in Illinois (the others being from Stevenson and Kaneland) to be rated nationally. This team is an Honorable Mention team, which only 5% of all teams nationally attain. They will split a $1000 scholarship for their efforts. Congrats to both teams for a job well done!
Subscribe to:
Posts (Atom)